Convergent Functions
We have seen convergent sequences where as the index \(n\) of the sequence approaches infinity, the sequence converges to a limit \(L\). We have also seen that this concept of convergence exists for series, allowing us to define convergent series. In this section we will look at the concept of convergence for functions.
Accumulation Points
Before we can define the limit of a function, we need to understand the concept of accumulation points or also often called limit points. An accumulation point of a set \(D\) is a point \(x_0\) such that every neighborhood of \(x_0\) contains at least one point of \(D\) different from \(x_0\), more formally \(x_0\) is an accumulation point of \(D\) if the following holds:
\[\forall \epsilon > 0 \quad ((x_0 - \epsilon, x_0 + \epsilon) \setminus \{x_0\}) \cap D \neq \emptyset \]If we define \(D=\{0\} \cup (1,2)\), then \(x_0=0\) is not an accumulation point of \(D\) since we can take the neighborhood where \(\epsilon=1\) and we have \((0-1,0+1) \setminus \{0\}\) which is \((-1,1)\) except for the point \(0\) and this neighborhood does not contain any point of \(D\). They nearly touch at the point \(1\) but don’t. The same would hold for \(\epsilon=0.5\) and so on so \(0\) is not an accumulation point of \(D\).
However, if we take \(x_0=1\), then for any \(\epsilon>0\) we have \((1-\epsilon,1+\epsilon) \setminus \{1\}\) which is guaranteed to contain some point larger than \(1\). Because our contains the interval \((1,2)\), there is also a point larger than \(1\) in the interval \((1,2)\) and hence \(1\) is an accumulation point of \(D\).
The reverse is also true, if we take \(x_0=2\), then for any \(\epsilon>0\) we have \((2-\epsilon,2+\epsilon) \setminus \{2\}\) which is guaranteed to contain some point smaller than \(2\) and again because our set contains the interval \((1,2)\), there is also a point smaller than \(2\) in the interval \((1,2)\) and hence \(2\) is an accumulation point of \(D\).
This is actually the case for any point in the interval \([1,2]\) and hence the set of all accumulation points of \(D\) denoted as \(D'\) is \(D'=[1,2]\).
Another example would be if we take the set \(D=(1,2) \cup (3,5)\). Then the set of all accumulation points of \(D\) is \(D'=[1,2] \cup [3,5]\). For the points between 2 and 3, so \(x \in (2,3)\), we can show that they are not accumulation points. Because if we pick any \(\epsilon > 0\) less or equal to the following value we don’t have any points in the neighborhood of \(x\) that are also in \(D\):
\[\epsilon = \frac{\min(3-x,x-2)}{2} \]So for example if we take \(x=2.2\) we take the minimum of \(3-2.2=0.8\) and \(2.2-2=0.2\) which is \(0.2\) and we can take \(\epsilon=0.1\). So we have \((2.2-0.1,2.2+0.1) \setminus \{2.2\}\) which is \((2.1,2.3)\) and this neighborhood does not contain any point of \(D\). So \(x=2.2\) is not an accumulation point of \(D\). The same would hold for any point in the interval \((2,3)\). To illustrate this we could take \(x=2.001\). The minimum of \(3-2.001=0.999\) and \(2.001-2=0.001\) is \(0.001\) and we can take \(\epsilon=0.0005\) to then have \((2.001-0.0005,2.001+0.0005) \setminus \{2.001\}\) which is \((2.0005,2.0015)\) and this neighborhood does not contain any point of \(D\). So \(x=2.001\) is not an accumulation point of \(D\).
Limit of a Function
Now that we understand the concept of accumulation points, we can define the limit of a function. First we define the function \(f\) on a set \(D \subseteq \RR\) as a mapping from \(D\) to \(\RR\):
\[f:D \to \RR \]if \(x_0 \RR\) is then an accumulation point of \(D\) then we write that the function \(f\) has a limit \(L\) at the point \(x_0\) as follows:
\[\lim_{x \to x_0}{f(x)}=L \]if for every \(\epsilon > 0\) there exists a \(\delta > 0\) such that the following holds:
\[\forall \epsilon > 0 \quad \exists \delta > 0 \quad \forall x \in ((x_0 - \delta, x_0 + \delta) \setminus \{x_0\}) \cap D \quad |f(x) - L| < \epsilon \]Because we know that \(x_0\) is an accumulation point of \(D\) we know that there exists at least one point \(x\) in the neighborhood of \(x_0\) that is also in \(D\). We can interpret the definition of the limit of a function similarly to the epsilon-delta definition of continuity. As we approach the point \(x_0\) from both sides, so making \(\delta\) smaller and smaller, the function \(f(x)\) approaches the limit \(L\). Or in other words, for any \(\epsilon\)-neighborhood of \(L\) we can find a point \(x\) in the neighborhood of \(x_0\) such that \(f(x)\) is in the \(\epsilon\)-neighborhood of \(L\). The requirement for the point \(x_0\) to be an accumulation point of \(D\) is important because if it is not, then we may not be able to find a point \(x\) where \(f(x)\) is in the \(\epsilon\)-neighborhood of \(L\).
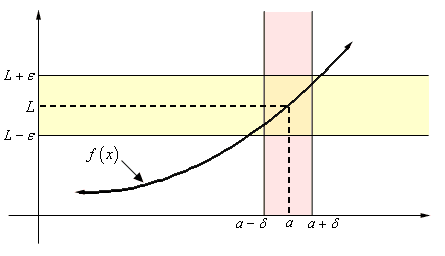
To be done
Another way of defining the limit of a function is to use sequences. If \(x_0\) is an accumulation point of \(D\) and we take any sequence \(a_n\) in \(D \setminus \{x_0\}\) such that the sequence converges to \(x_0\) as \(n\) approaches infinity, so \(\lim_{n \to \infty} a_n = x_0\), then we can say that the limit of the function \(f\) at the point \(x_0\) is equal to the limit of the sequence \(a_n\) as \(n\) approaches infinity:
\[\lim_{n \to \infty} f(a_n) = L \]The idea is that as the sequence \(a_n\) approaches the point \(x_0\), the function \(f(a_n)\) approaches the limit \(L\). So in a way we are again saying that the function \(f\) approaches the limit \(L\) as we approach the point \(x_0\).
We are given the function \(f(x) = 2x\) and we want to inspect the limit at the point \(x_0=0\). We can take the sequence \(a_n = \frac{1}{n}\) which converges to \(0\) as \(n\) approaches infinity. We can then calculate the limit of the function at the point \(x_0=0\) by substituting the sequence into the function:
\[\lim_{x \to 0} f(x) = \lim_{n \to \infty} f(a_n) = \lim_{n \to \infty} f(\frac{1}{n}) = \lim_{n \to \infty} 2(\frac{1}{n}) = 0 \]So we can say that the limit of the function \(f\) at the point \(x_0=0\) is \(0\). We can also take the sequence \(a_n = -\frac{1}{n}\) which also converges to \(0\) as \(n\) approaches infinity. Again applying the sequence to the function we get:
\[\lim_{x \to 0} f(x) = \lim_{n \to \infty} f(a_n) = \lim_{n \to \infty} f(-\frac{1}{n}) = \lim_{n \to \infty} 2(-\frac{1}{n}) = 0 \]From this definition it also becomes rather clear that the function \(f\) is also continuous at the point \(x_0\) if the limit of the function at the point \(x_0\) is equal to the value of the function at the point \(x_0\), so \(f(x_0) = L\). Importantly the limit at \(x_0\) does not have to be defined, but if it does exist and it is not equal to the value of the function at the point \(x_0\), then we say that the function has a discontinuity at the point \(x_0\). However, if a function is continuous at the point \(x_0\), then the limit of the function at the point \(x_0\) is equal to the value of the function at the point \(x_0\) and therefore the limit exists.
We are given the following function:
\[f(x) = \begin{cases} x & \text{if } x \neq 2 \\ 3 & \text{if } x = 2 \end{cases} \]Then the limit of the function as we approach the point \(x_0=2\) is \(2\), but the value of the function at the point \(x_0=2\) is \(3\). So we can say that the function has a discontinuity at the point \(x_0=2\) because the limit of the function at the point \(x_0=2\) is not equal to the value of the function at the point \(x_0=2\).

What about accumulation points at the point \(x_0=\infty\)? or if we have a function that is not defined at \(x_0\)?
If we have two functions \(f\) und \(g\), that are both defined on a set \(D\) and both have the same the limits \(A\) and \(B\) at the point \(x_0\) so we have:
\[\lim_{x \to x_0}{f(x)} = A \quad \text{and} \quad \lim_{x \to x_0}{g(x)} = B \]then we can also define the following limits:
- Sum/Difference of Functions: The limit of the sum of the two functions at the point \(x_0\) is equal to the sum of the limits of the two functions at the point \(x_0\): \(\lim_{x \to x_0}{(f(x) \pm g(x))} = A \pm B\).
- Product of Functions: The limit of the product of the two functions at the point \(x_0\) is equal to the product of the limits of the two functions at the point \(x_0\): \(\lim_{x \to x_0}{(f(x) * g(x))} = A * B\).
Squeeze Theorem for Limits
There is similar version of the Squeeze theorem of sequences for limits of functions. If we have three functions \(a,b,f\) that are all defined on a set and we have the following function inequality:
\[a(x) \leq f(x) \leq b(x) \quad \text{for all } x \in D \]If we then have the following limits at the point \(x_0\):
\[\lim_{x \to x_0}{a(x)} = \lim_{x \to x_0}{b(x)} = L \]then we can conclude that the limit of the function \(f\) at the point \(x_0\) is also equal to \(L\):
\[\lim_{x \to x_0}{f(x)} = L \]We can look at the following function:
\[f(x) = \frac{\sin(x)}{x} \]We know that this function is not defined at the point \(x_0=0\) because we would have a division by zero. However, we can still look at the limit of the function as we approach the point \(x_0=0\). We can use the Squeeze theorem to find this limit. Specifically we look at it for \(0 \leq x \leq \sqrt{6}\).
Don’t get how this example works?
Left and Right Limits
If we have the function \(f\) defined on a set \(D \subseteq \RR\) then we can actually define two different limits at the point \(x_0\) depending on the direction from which we approach the point \(x_0\), these limits are called the left limit and the right limit. We do this by changing the domain of the function \(f\) to only include points that are either smaller or larger than \(x_0\). More specifically we define the left limit of the function \(f\) at the point \(x_0\) as follows:
\[\lim_{x \to x_0^-}{f(x)} = L \]where \(x\) is only in the limited domain \(D^- = \{x \in D \mid x < x_0\} = D \cap (-\infty, x_0)\). We can also do the same for the right limit of the function \(f\) at the point \(x_0\):
\[\lim_{x \to x_0^+}{f(x)} = L \]where \(x\) is only in the limited domain \(D^+ = \{x \in D \mid x > x_0\} = D \cap (x_0, \infty)\). If the left limit and the right limit are equal, then we say that the function is continuous at the point \(x_0\) and therefore the limit of the function at the point \(x_0\) is equal to the value of the function at the point \(x_0\):
\[\lim_{x \to x_0^-}{f(x)} = \lim_{x \to x_0^+}{f(x)} \implies \lim_{x \to x_0}{f(x)} = f(x_0) \]Let’s consider the following function:
\[f(x) = \begin{cases} cos(x) & \text{if } x \geq 0 \\ x + 1 & \text{if } x < 0 \end{cases} \]Then we know that the cosine function is continous for all \(x > 0\) and the function \(x + 1\) is continuous for all \(x < 0\). The question remains what happens at the point \(x_0=0\). We can look at the left limit and the right limit of the function at the point \(x_0=0\). The left limit is defined as follows:
\[\lim_{x \to 0^-}{f(x)} = \lim_{x \to 0^-}{(x + 1)} = 1 \]The right limit is defined as follows:
\[\lim_{x \to 0^+}{f(x)} = \lim_{x \to 0^+}{cos(x)} = cos(0) = 1 \]Because the cosine function is defined at the point \(x_0=0\) and the value of the function at the point \(x_0=0\) is also equal to \(1\), we can say that the function is continuous at the point \(x_0=0\). So we have:
\[\lim_{x \to 0}{f(x)} = 1 \]However, this does not normally have to be the case. If the left limit and the right limit are not equal, then we say that the function has a discontinuity at the point \(x_0\).
Going to Infinity
We say a function has an infinite limit at the point \(x_0\) if the function approaches infinity as we approach the point \(x_0\). More formally, we say that the limit of the function \(f\) at the point \(x_0\) is equal to infinity if for every \(T > 0\) there exists a \(\delta > 0\) such that the following holds for all \(x \in D \setminus \{x_0\}\):
\[\lim_{x \to x_0}{f(x)} = \infty \quad \text{if} \quad |x - x_0| < \delta \quad \implies \quad f(x) > T \]The same goes for negative infinity if we change the condition to \(f(x) < -T\):
\[\lim_{x \to x_0}{f(x)} = -\infty \quad \text{if} \quad |x - x_0| < \delta \quad \implies \quad f(x) < -T \]This can be interpreted that for any positive number \(T\) we can find a neighborhood around the point \(x_0\) such that all points in this neighborhood have a function value larger than \(T\). This means that as we approach the point \(x_0\), the function value gets larger and larger without bound.
Let’s consider the function \(f(x) = \frac{1}{x}\) as \(x\) approaches \(0\). The function is not defined at the point \(x_0=0\) because we would have a division by zero. However, we can still look at the limit of the function as we approach the point \(x_0=0\). We can do this by looking at the left limit and the right limit of the function at the point \(x_0=0\).
The left limit is defined as follows:
\[\lim_{x \to 0^-}{f(x)} = \lim_{x \to 0^-}{\frac{1}{x}} = -\infty \]The right limit is defined as follows:
\[\lim_{x \to 0^+}{f(x)} = \lim_{x \to 0^+}{\frac{1}{x}} = \infty \]Because we can pick for any positive number \(T\) the delta to be \(\frac{1}{T}\).
The limit of the natural logarithm function \(f(x) = \ln(x)\) as \(x\) approaches \(0\) from the right is also equal to negative infinity.
Limits at Infinity
If we have a function \(f\) that is defined on a set \(D \subseteq \RR\) and it is unbounded, then we can define the limit of the function at infinity. We say that the limit of the function \(f\) at infinity is equal to \(L\) if for every \(\epsilon > 0\) there exists a \(c > 0\) for all \(x \in D\) such that the following holds:
\[x > c \quad \implies \quad |f(x) - L| < \epsilon \]We denote this as:
\[\lim_{x \to \infty}{f(x)} = L \]This definition means for any \(\epsilon\)-neighborhood of \(L\), we can find a point \(c\) such that for all points \(x\) larger than \(c\), the function \(f(x)\) is in the \(\epsilon\)-neighborhood of \(L\).
Doesn’t make a lot of sense to me.
We can equivalently define the limit of the function \(f\) at negative infinity by changing the condition to \(x < -c\). So \(\lim_{x \to -\infty}{f(x)} = L\) if the following holds:
\[x < -c \quad \implies \quad |f(x) - L| < \epsilon \]Let’s consider the function \(f(x) = \frac{1}{x}\) as \(x\) approaches infinity. We want to find the limit:
\[\lim_{x \to \infty}{f(x)} = \lim_{x \to \infty}{\frac{1}{x}} \]We can see that as \(x\) gets larger and larger, the value of \(f(x)\) gets closer and closer to \(0\). So we can say that the limit of the function \(f\) at infinity is \(0\).
Can we actually show this better?